TAREA #2

TAREA No. 2

1.SISTEMAS NUMÉRICOS: 

• DECIMAL
• BINARIO
• OCTAL
• HEXADECIMAL

2.CONVERSIÓN ENTRE SISTEMAS NUMÉRICOS

1. SISTEMAS NUMERICOS:

• DECIMAL:

El sistema de numeración decimal es un sistema posicional.  En este sistema utilizamos diez dígitos, que son: 0, 1, 2, 3, 4, 5, 6, 7, 8, y 9. Por ello decimos que el sistema decimal es de base diez. En este sistema, cada cifra representa un valor distinto dependiendo de su ubicación en el número.

VALOR POSICIONAL

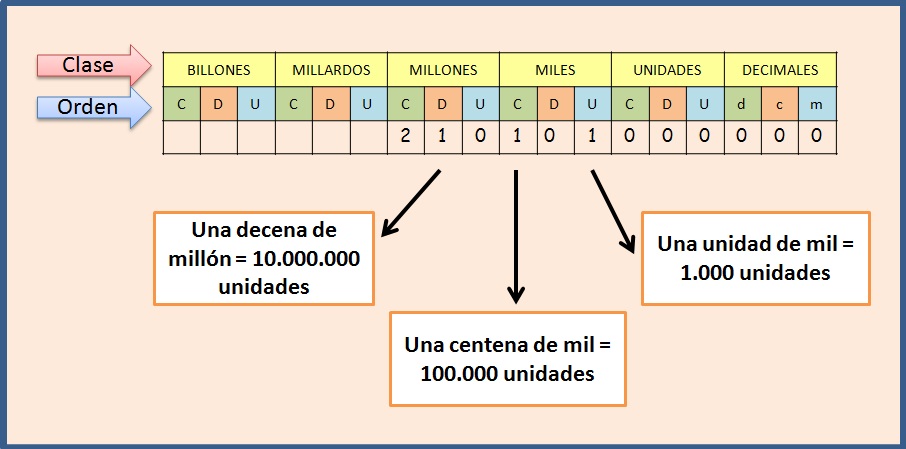
El valor posicional de un dígito es un número natural o decimal es el valor que toma una cifra de acuerdo con la posición que ocupa en un número. Como se mencionó Anteriormente, en el Sistema de numeración Decimal  utilizamos diez dígitos:  0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. Estos dígitos toman un valor diferente dependiendo del lugar que ocupen en el número. Por el ejemplo, el dígito 1 en el número 210.101.000 tiene tres valores diferentes: 

• BINARIO:

•El sistema de numeración binario solo tiene dos dígitos. El sistema binario con sus dos dígitos es un sistema en base dos. Los dígitos binarios (bits) son 0 y 1. 
• La posición de un 1 o de un 0 en un número binario indica su peso, o valor dentro del número, así como la posición de un dígito decimal determina el valor de ese dígito. 

• Los pesos de un número binario están basados en las potencias de dos.

• OCTAL:

El sistema numérico en base 8 se llama octal y utiliza los dígitos del 0 al 7. En informática a veces se utiliza la numeración octal en vez de la hexadecimal. Tiene la ventaja de que no requiere utilizar otros símbolos diferentes de los dígitos. Sin embargo, para trabajar con bytes o conjuntos de ellos, asumiendo que un byte es una palabra de 8 bits, suele ser más cómodo el sistema hexadecimal, por cuanto todo byte así definido es completamente representable por dos dígitos hexadecimales.

Decimal	Binario	Hexadecimal	octal
0	00000	0	0
1	00001	1	1
2	00010	2	2
3	00011	3	3
4	00100	4	4
5	00101	5	5
6	00110	6	6
7	00111	7	7
8	01000	8	10
9	01001	9	11
10	01010	A	12
11	01011	B	13
12	01100	C	14
13	01101	D	15
14	01110	E	16
15	01111	F	17
16	10000	10	20
17	10001	11	21
18	10010	12	22
19	10011	13	23
20	10100	14	24
21	10101	15	25
22	10110	16	26
23	10111	17	27
24	11000	18	30
25	11001	19	31
26	11010	1A	32
27	11011	1B	33
28	11100	1C	34
29	11101	1D	35
30	11110	1E	36
31	11111	1F	37
32	100000	20	40
33	100001	21	41

• HEXADECIMAL

El sistema hexadecimal (abreviado como 'Hex', no confundir con sistema sexagesimal) es el sistema de numeración posicional que tiene como base el 16. Su uso actual está muy vinculado a la informática y ciencias de la computación donde las operaciones de la CPU suelen usar el byte u octeto como unidad básica de memoria; y, debido a que un byte representa ${\displaystyle 2^{8}}$ valores posibles, y esto puede representarse como 

${\displaystyle 2^{8}=2^{4}\cdot 2^{4}=16\cdot 16=}$ ${\displaystyle 1\cdot 16^{2}+0\cdot 16^{1}+0\cdot 16^{0}}$, que equivale al número en base 16 ${\displaystyle 100_{16}}$, dos dígitos hexadecimales corresponden exactamente a un byte.

En principio, dado que el sistema usual de numeración es de base decimal y, por ello, sólo se dispone de diez dígitos, se adoptó la convención de usar las seis primeras letras del alfabeto latino para suplir los dígitos que nos faltan. El conjunto de símbolos es el siguiente:

${\displaystyle S=\{0,1,2,3,4,5,6,7,8,9,\mathrm {A} ,\mathrm {B} ,\mathrm {C} ,\mathrm {D} ,\mathrm {E} ,\mathrm {F} \}\,}$

Se debe notar que A = 10, B = 11, C = 12, D = 13, E = 14 y F = 15. En ocasiones se emplean letras minúsculas en lugar de mayúsculas. Como en cualquier sistema de numeración posicional, el valor numérico de cada dígito es alterado dependiendo de su posición en la cadena de dígitos, quedando multiplicado por una cierta potencia de la base del sistema, que en este caso es 16. Por ejemplo: 3E0A₁₆ = 3×16³ + E×16² + 0×16¹ + A×16⁰ = 3×4096 + 14×256 + 0×16 + 10×1 = 15882.

El sistema hexadecimal actual fue introducido en el ámbito de la computación por primera vez por IBM en 1963. Una representación anterior, con 0-9 y u-z, fue usada en 1956 por la computadora Bendix G-15.

Hexadecimal	Decimal
A	10
B	11
C	12
D	13
E	14
F	15

2. CONVERSIÓN ENTRE SISTEMAS NUMÉRICOS

• Conversión de Decimal a Binario

Otra forma de obtener el numero decimal a binario es realizar lo siguiente:

Convertir un número decimal al sistema binario es muy sencillo: basta con realizar divisiones sucesivas por 2 y escribir los restos obtenidos en cada división en orden inverso al que han sido obtenidos.

Por ejemplo, para convertir al sistema binario el número decimal 77 haremos una serie de divisiones que arrojarán los restos siguientes:

77 / 2 = 38 Resto: 1

38 / 2 = 19 Resto: 0

19 / 2 = 9 Resto: 1

9 / 2 = 4 Resto: 1

4 / 2 = 2 Resto: 0

2 / 2 = 1 Resto: 0

1 / 2 = 0 Resto: 1

y, tomando los restos en orden inverso obtenemos la cifra binaria:

Decimal 77 = Binario 1001101

• Conversión de un número decimal a octal

La conversión de un número decimal a octal se hace con la misma técnica que ya hemos utilizado en la conversión a binario, mediante divisiones sucesivas por 8 y colocando los restos obtenidos en orden inverso. Por ejemplo, para escribir en octal el número decimal 122 tendremos que hacer las siguientes divisiones:

122 / 8 = 15     Resto: 2

15 / 8 = 1           Resto: 7

1 / 8 = 0               Resto: 1

Tomando los restos obtenidos en orden inverso tendremos la cifra octal:

Decimal 122 =  Octal 172

• Conversión de un número decimal a hexadecimal

Utilizando la técnica habitual de divisiones sucesivas, la conversión de un número decimal a hexadecimal. Por ejemplo, para convertir a hexadecimal del número decimal 1735 será necesario hacer las siguientes divisiones:

1735 / 16 = 108    Resto: 7

108 / 16 = 6           Resto: C es decir, 12 en decimal

6 / 16 = 0                Resto: 6

De ahí que, tomando los restos en orden inverso, resolvemos el número en hexadecimal:

decimal 1735 = hexadecimal 6C7

AUTOR: AZIEL OMAR TARACENA PELAYO